Braided rivers as changing states: from images to probabilistic forecasts
Braided rivers appear chaotic at first sight, but their complexity hides repeating patterns. In my doctoral thesis, I developed a method that discovers these patterns from images and uses them to build probabilistic forecasts of sediment transport. The goal is to show that river form can be translated into a language of states, and that this language can be used to generate reliable, data driven predictions.
By Clemente Gotelli
Braided rivers change continuously. Even with constant water and sediment supply, they reorganize their channels as bars migrate, bifurcations open or close, and new flow paths form. This reworking produces intense variability in sediment transport and makes these rivers difficult to predict with standard deterministic models.
My thesis introduces a new approach based on two ideas. First, the river does not explore an infinite range of shapes. Instead, it cycles through a limited set of recurrent morphological states. Second, the transitions among these states can be described with a continuous time Markov chain. Once the states are known, and once their transition probabilities are estimated, the Markov model becomes a generator capable of simulating many possible futures for the river. From these synthetic futures, we can derive probabilistic forecasts of sediment flux that incorporate uncertainty directly.
A laboratory river observed minute by minute
The dataset comes from a long duration experiment in a 3.3 meter by 1 meter flume filled with uniform sand. Steady discharge and sediment supply created a self sustaining braided pattern that evolved freely for nearly 1,200 hours. A camera captured one image every minute, and a load cell recorded the downstream sediment flux in real time.

The experimental flume used in the study.
The resulting time series shows the type of intermittency that motivates a probabilistic view. Long periods of low activity alternate with sharp spikes in transport. Even over hundreds of hours, the cumulative flux does not settle to a simple trend.
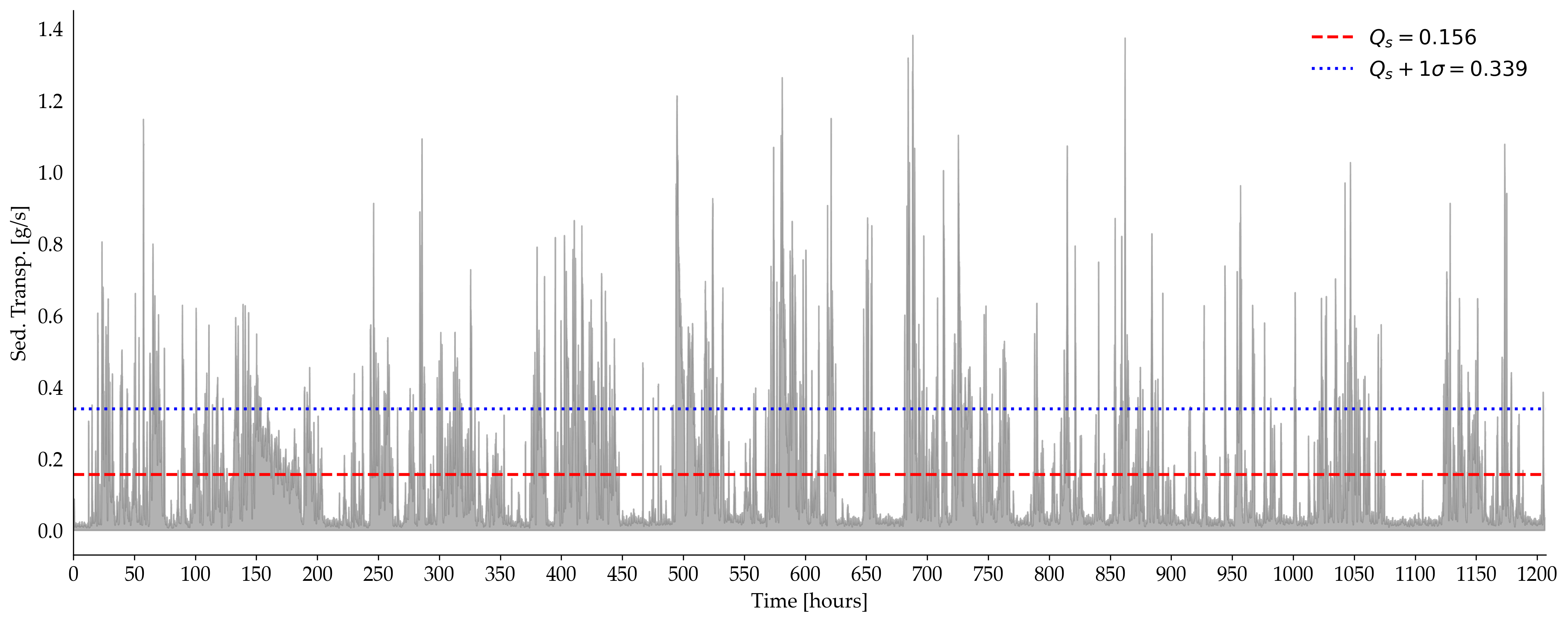
Intermittent sediment transport measured during the experiment.
Converting images into a set of morphological states
Each photograph is processed to highlight the wetted area of the channel. A color filter isolates the dyed water and produces a clean binary mask that separates water from dry bed. A one pixel water outline is then extracted to represent the planform shape in a consistent and stable way.
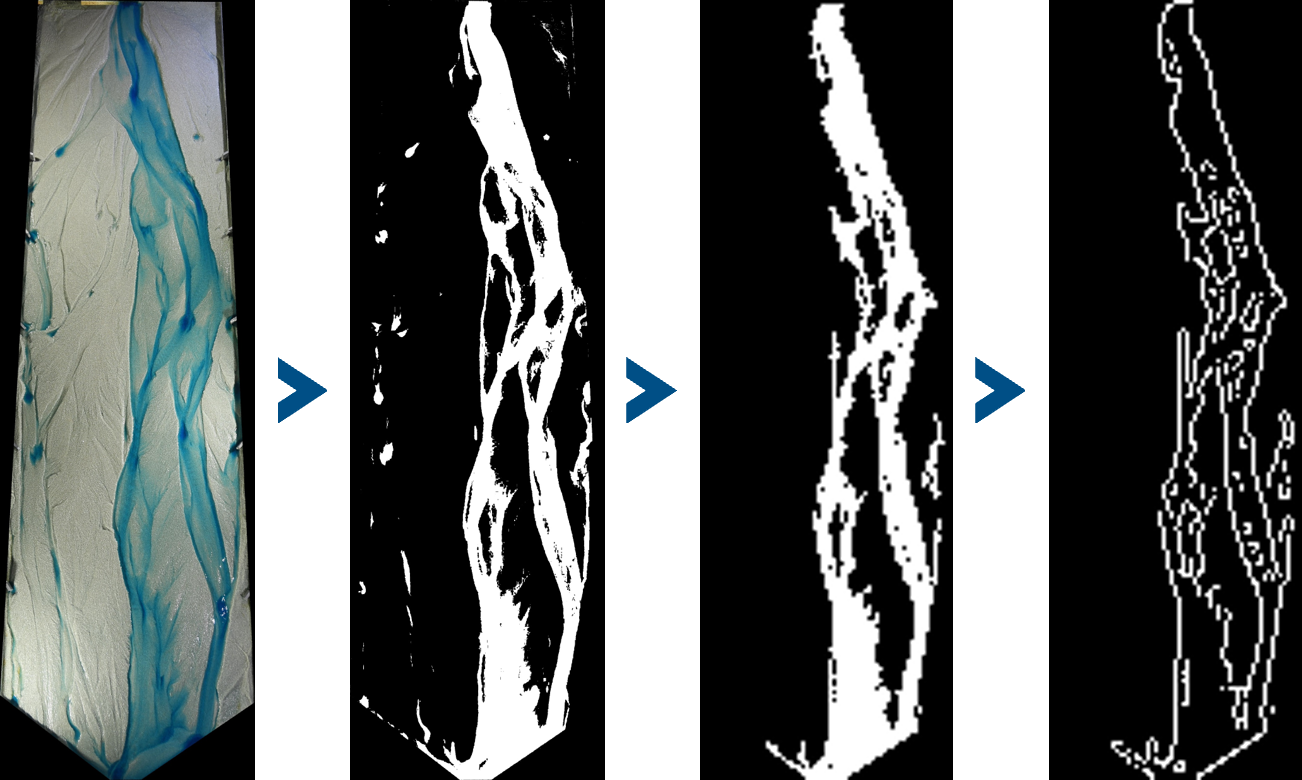
Image processing steps from raw photograph to water outline.
To compare two river configurations, the method uses a combination of the Modified Hausdorff Distance and the Dice index. These two distances are combined into a single matrix and projected into a low dimensional morpho space through dimensionality reduction. Clustering in this space reveals that the river cycles through exactly sixteen recurrent morphological states. These include narrow channels, transitional structures, and wide multi thread patterns rich in bars.
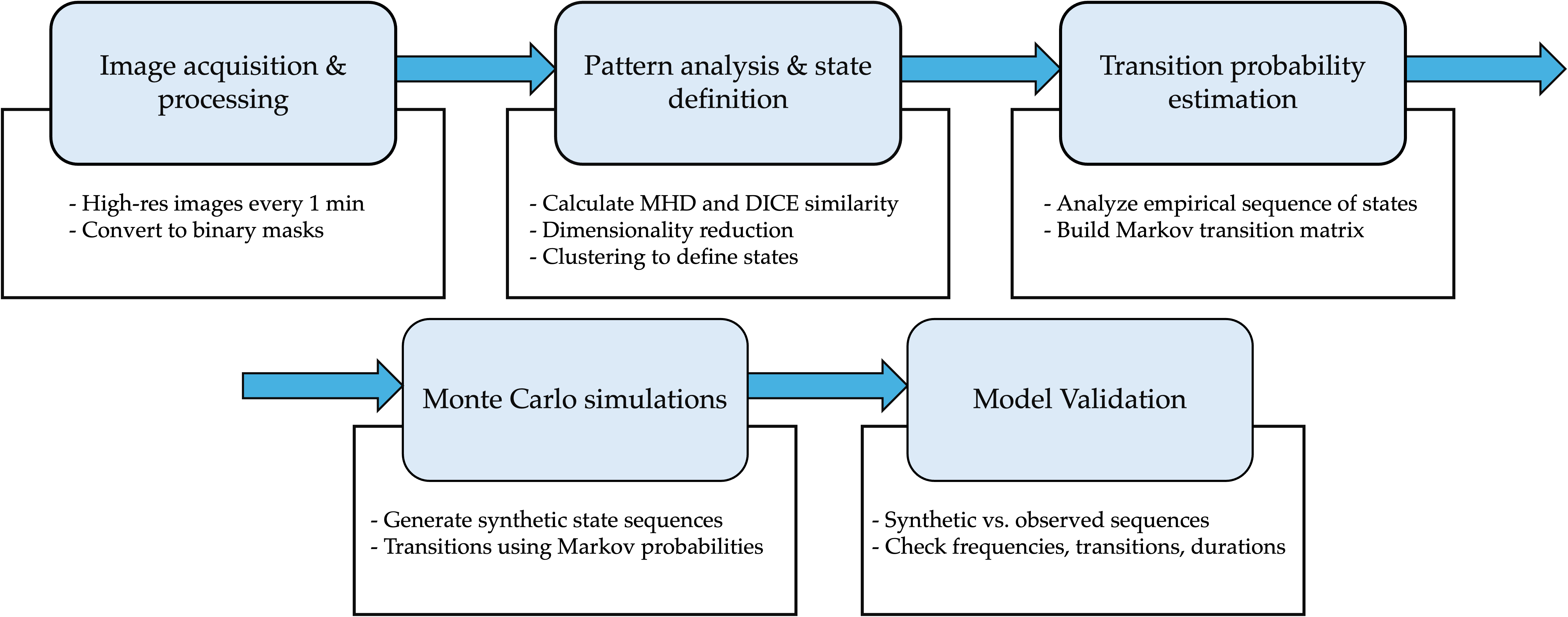
Workflow from images to a Markov chain model.
What these states reveal about sediment transport
Because each image has a corresponding measurement of bedload, we can estimate the typical transport rate within each state. The result is consistent across the entire dataset. Narrow states export sediment more efficiently and with higher variability. Wide braided states tend to store sediment and produce lower and steadier fluxes. This confirms that morphology contains predictive information about transport.
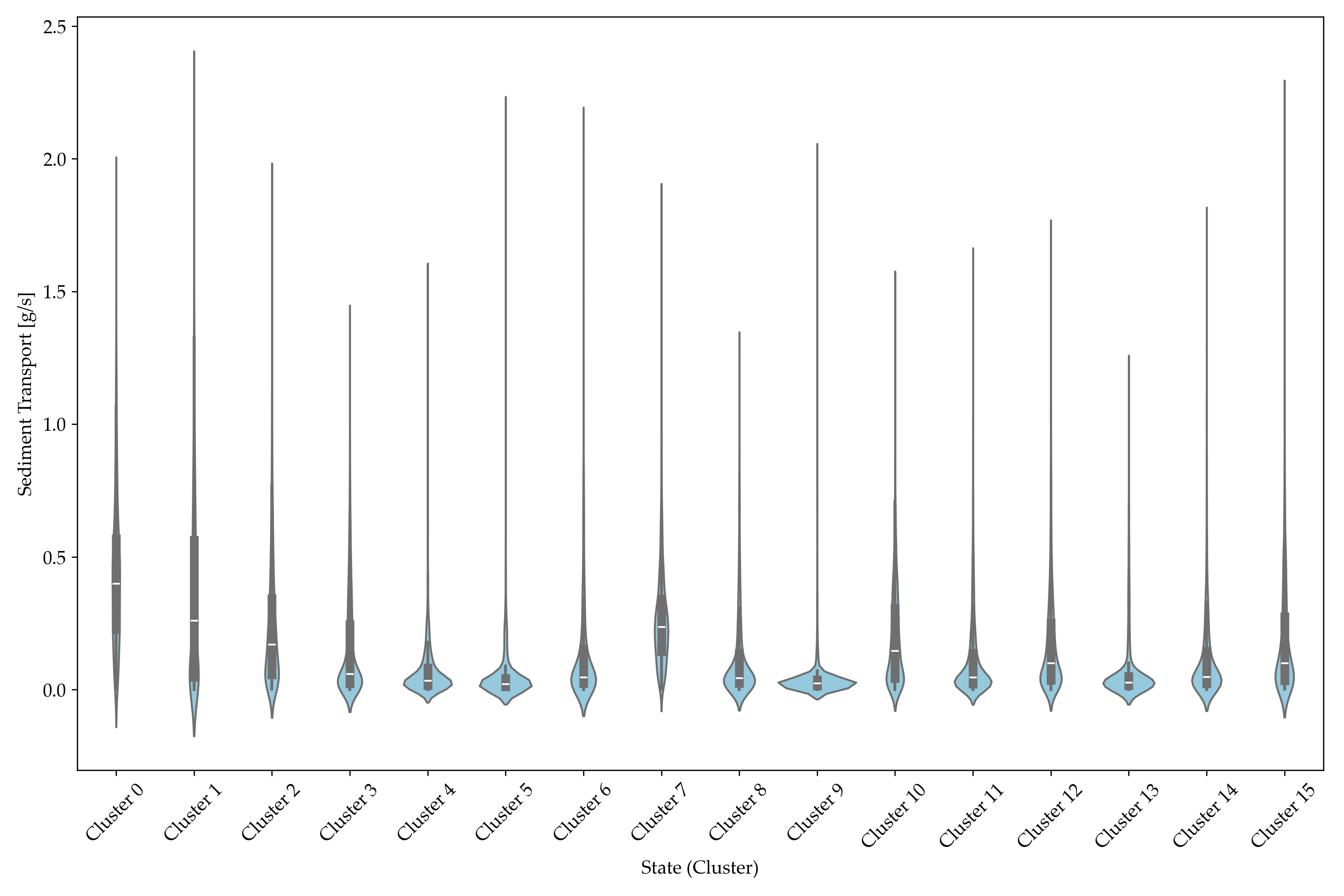
Transport distributions for the sixteen morphological states.
A Markov chain for state transitions
Once every minute of the experiment has a state label, the river can be viewed as a sequence of state visits. Some states persist for long periods while others act as brief intermediates during reorganizations. This behavior can be represented by a continuous time Markov chain in which each state has a characteristic dwell time and a distribution of possible next states.
The transition matrix shows that bar rich states are stable and long lived. In contrast, simple narrow states are short lived but crucial for routing sediment out of the system. The same pattern appears in two shorter independent runs, which validates the robustness of the state definitions and transition structure.
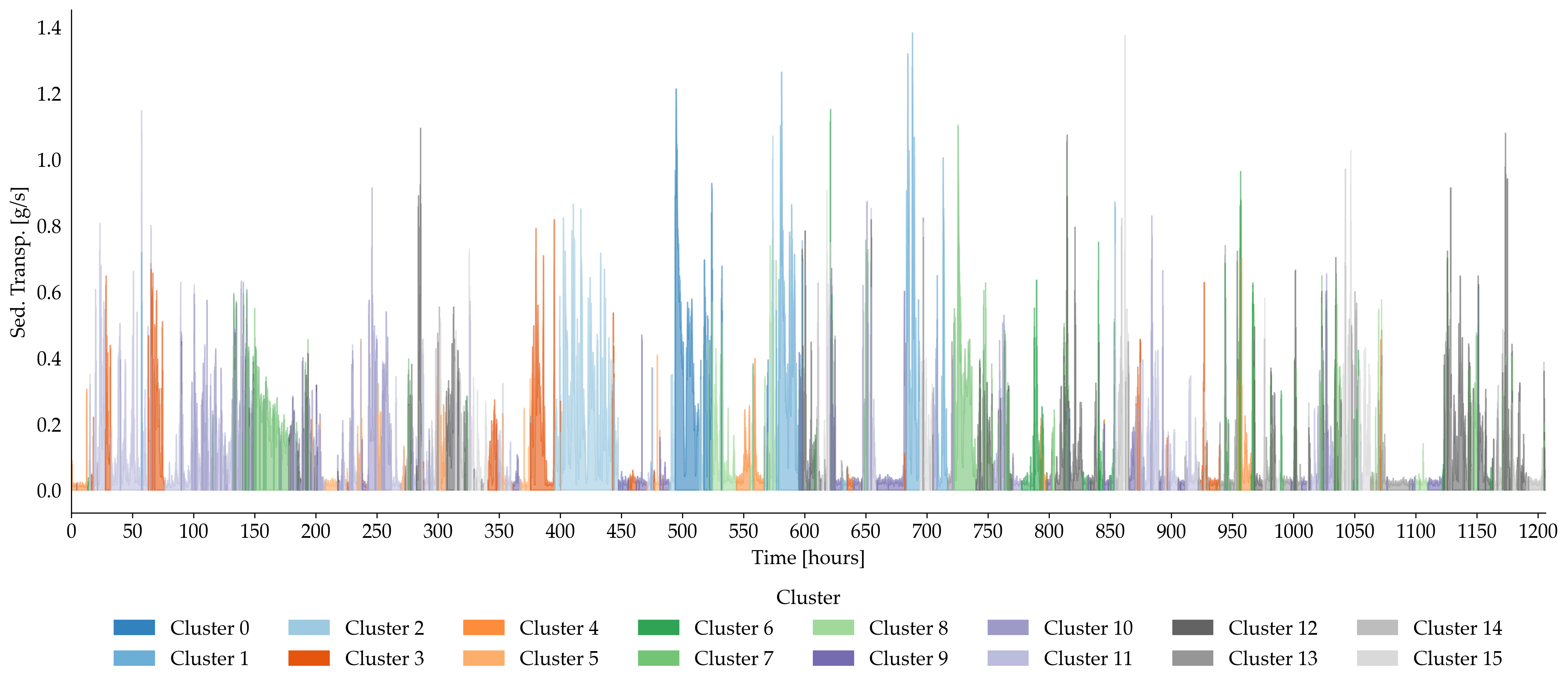
Time series of sediment transport colored by morphological state.
Monte Carlo as the engine of probabilistic forecasting
The most important part of the framework is the Monte Carlo generator. Once the Markov chain is calibrated, we simulate a very large number of synthetic futures. Each simulation is a possible trajectory of state transitions that respects the observed transition probabilities and dwell time distributions.
These synthetic trajectories form the backbone of the forecast. For every simulated sequence of states, we reconstruct a sediment transport time series by sampling from the empirical distribution of each state. This two layer Monte Carlo process produces a large ensemble of transport signals. From this ensemble, we can compute confidence intervals, return levels, and the distribution of possible future bursts.
The synthetic series reproduce the real experiment remarkably well. They capture the mean, the variance, the timing structure of bursts, and the scaling of variability across time scales. They also highlight a small mismatch at very low frequencies, which identifies a clear direction for future improvement using semi Markov models.
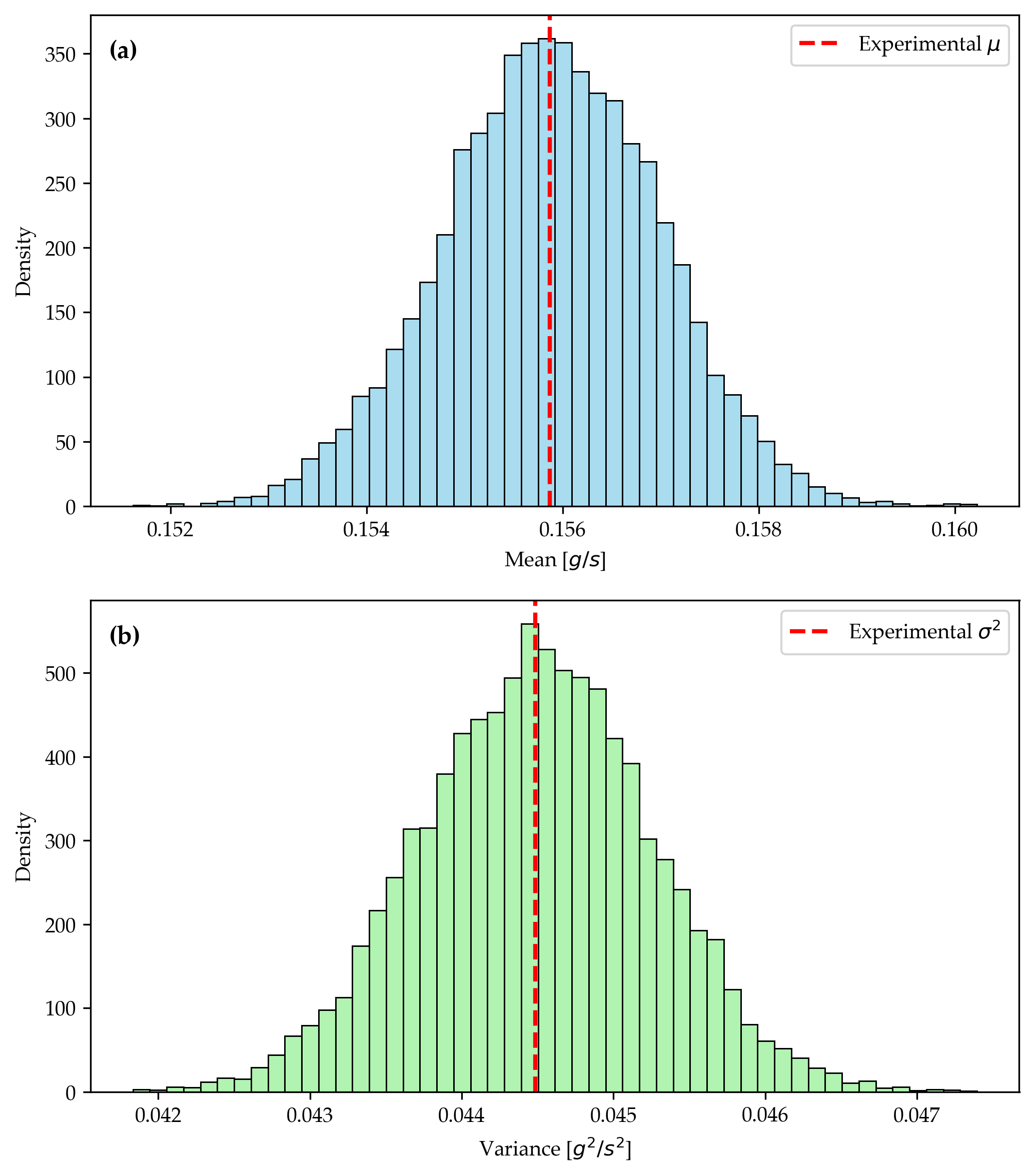
Experimental vs synthetic transport series showing close agreement.
Why this method represents a new direction
The thesis presents the first complete pipeline that begins with planview images, identifies recurrent morphological states, models their temporal evolution with a continuous time Markov chain, generates synthetic futures with a Monte Carlo engine, and reconstructs probabilistic forecasts of sediment transport.
This approach fills a gap between descriptive metrics that cannot predict future behavior and detailed physics based models that are difficult to use for uncertainty quantification. The method is transparent and computationally light. It can be applied to any imagery based dataset, including satellite and drone observations, making it useful for regions where transport measurements are unavailable.
Most importantly, the results suggest that braided rivers do not behave randomly. They follow a structure defined by a small number of morphological states and by the probabilities of transitioning among them. This discovery opens new possibilities for understanding how form relates to function and for developing probabilistic theories of river dynamics.
If you want to see more details, you may download the full thesis:
